The basic structure of the DAO's objective function iterates over all the students and sums up their `unhappinesses'.
There are two main types of constraints in the DAO's objective
function: Room-student and student-consensus related
errors (Table 2.1). Room-student constraints take student and
room attributes into account. For example, a room-student mismatch
occurs when a student's first choice hall does not match the hall of
their room. Student-consensus constraints are concerned only with the
students in the room (or suite). Student-consensus errors occur when
the occupants of the room do not agree, for example, a student who
prefers classical music is in the same room as someone who objects to
the classics. Student-consensus constraints can also be used to
determine the attribute of the room, such as non-smoking and
gender![]() .
.
|
Additionally, a compiled-in table determines whether constraints are weighted by students' seniority and reservation order. Priority increases the constraint penalty if there is a problem, thereby encouraging the system to find a better solution for the individual and the whole. `Dorm Preferences' and `Roommate Requests' are the weighted constraints in the DAO. A closer look into weighted and unweighted constraints follows in Section 2.2.1.
The Objective Function is the sum of all per-student constraint violations, weighted and unweighted, as they apply to each student in a bed, given all the other students in their beds. Housing sets the penalties to indicate the relative importance of the errors (e.g. no bed at all is much worse than a older roommate). The grades and the error breakdowns are kept on both individual and overall bases for reporting purposes.
The Objective Function (details in Appendix B), 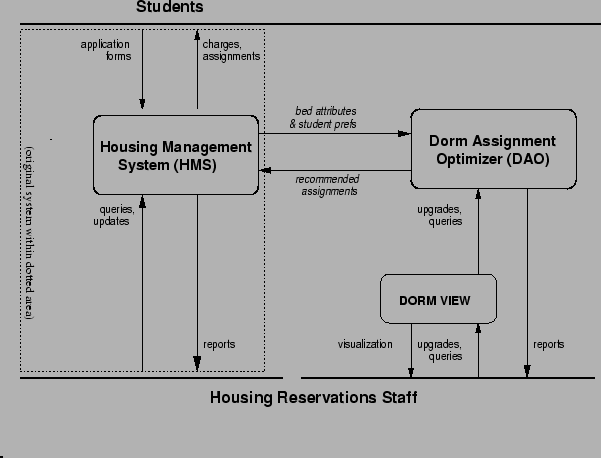 , is computed
as:
, is computed
as:
where 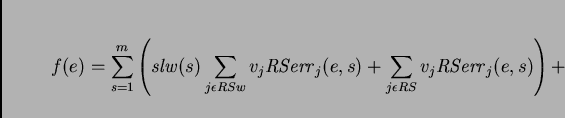 is the state,
is the state, 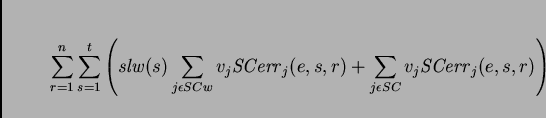 is the number of students,
is the number of students, ![]() is the number of rooms,
is the number of rooms, ![]() is the number of students in a room,
is the number of students in a room, ![]() is the student's calculated seniority-lottery-weight
is the student's calculated seniority-lottery-weight![]() ,
, ![]() is the user-specified value of the constraint coefficient,
is the user-specified value of the constraint coefficient, ![]() is
the set of weighted room-student constraints,
is
the set of weighted room-student constraints, ![]() is the set of
unweighted room-student constraints,
is the set of
unweighted room-student constraints, ![]() is a room-student error,
is a room-student error,
![]() is the set of weighted student-consensus constraints,
is the set of weighted student-consensus constraints, ![]() is
the set of unweighted student-consensus constraints, and
is
the set of unweighted student-consensus constraints, and ![]() is a
student-consensus error.
is a
student-consensus error.
The overall cost (the global grade or score) for all the students,
computed initially and as sanity checks, is linear in the number of
students. Most of the time, however, we can update it incrementally
in constant time by adding the change in cost resulting from a single
move to the global grade.![]() Our goal is to
minimize the global grade.
Our goal is to
minimize the global grade.
| Sometimes the Whole Must Suffer | ||
| A first time student for Fall 2000, seventh in line by lottery number, had three different hall choices, the second of which was the less popular all-female hall. The DAO placed her in her second choice for the overall benefit of those students who would not be happy with anything less than this student's first choice. Regardless, she was manually upgraded to her first choice because she was at the head of the line. | ||
Seniority weights, constraint error values, and other configurable
parameters assigned by Housing, are read from an options
file as the program begins, and are used to compute the overall cost
of the objective function. As management policy changes, these choices
can be amended without recompiling the DAO. However, choosing values
accurately to reflect these policies becomes the real challenge, as
shown in Section 4.1.1 (page
![]() ).
).