Methodology

Using the three datasets, we ran a series of 32 runs, using DAO versions v1.10 to v1.15, varying only the cooling schedules and the dataset. Each round within a term's dataset began with the same arbitrary placement of all students into available beds, followed by a randomization step. The objective function penalties remained constant, and each round used a different random number seed. All students were moveable and no beds were blocked. A minimization step in priority order followed each round.

Using non-parametric ranking methods which make no assumptions about the distribution of the samples, we calculate the mean rank of various approaches listed in Table 4.2 based on the ranks of their measurements rather than the measurements themselves.

Ranking the data from lowest to highest scores, we use the Kruskal-Wallis test, often called an ``analysis of variance by ranks'', for groups with three or more sample populations. For tied ranks, the rank assigned is the mean of the ranks they would have been assigned had they not been tied.

In each case, the null hypothesis asserts the populations are the same. If the test statistic is greater than 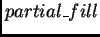$\alpha = .05$ (and in most cases .01), we reject the null hypothesis, and conclude the samples come from different populations.

To determine between which of the samples significant differences occur, multiple comparison tests of the rank means are made against the $Q_{\alpha,k}$ test statistic [Zar99].

The following sections present our specific investigations and observations.

Table 4.5: Statistics (in millions) from Fall 1998 Tests

Scheme	Avg Score	Std Dev	Avg Best	Std Dev	Avg Attempts
sa0	49.084	0.270	49.082	0.276	54.106
sa1	52.170	0.887	49.814	0.303	6.340
sa2	49.276	0.324	49.174	0.209	12.095
sa3	50.062	0.620	49.284	0.258	8.171
sa4	49.069	0.308	49.055	0.288	19.528
sigmet4	49.051	0.235	49.032	0.236	18.605
sigmet1	52.022	0.857	49.741	0.366	6.162
rldhc	49.121	0.244	49.115	0.248	42.526
mr	667.506	10.266	667.506	10.266	40.000
m	671.013	7.197	671.013	7.197	40.000
r	933.03	11.232	933.03	11.232	.100

Table 4.3: Statistics (in millions) from Fall 2000 Tests

Scheme	Avg Score	Std Dev	Avg Best	Std Dev	Avg Attempts
sa0	88.685	0.188	88.683	0.194	43.376
sa1	92.640	0.872	89.306	0.238	8.379
sa2	88.858	0.292	88.777	0.226	17.735
sa3	89.281	0.498	88.722	0.189	13.019
sa4	88.629	0.243	88.620	0.229	27.608
sigmet4	88.570	0.214	88.562	0.213	26.884
sigmet1	92.998	1.015	89.362	0.256	8.482
rldhc	88.750	0.221	88.743	0.218	43.361
mr	867.751	8.405	867.751	8.405	40.000
m	863.249	7.132	863.249	7.132	40.000
r	1156.37	35.924	1156.37	35.924	.100

Table 4.4: Statistics (in millions) from Fall 1999 Tests

Scheme	Avg Score	Std Dev	Avg Best	Std Dev	Avg Attempts
sa0	71.336	0.831	71.329	0.839	44.162
sa1	75.310	1.080	72.049	0.881	9.182
sa2	71.078	0.520	71.062	0.514	19.830
sa3	71.606	0.895	71.268	0.760	14.021
sa4	71.193	0.805	71.173	0.803	31.728
sigmet4	71.077	0.740	71.071	0.734	31.255
sigmet1	74.810	1.209	71.788	0.807	9.102
rldhc	70.992	0.544	70.987	0.533	43.772
mr	836.634	5.462	836.634	5.462	40.000
m	838.684	5.437	838.684	5.437	40.000
r	1125.95	13.412	1125.95	13.412	.100

download thesis